The Gauntlet: Robot Navigation using Math

The culmination of Olin College of Engineering’s first year course Quantitative Engineering Analysis, the Gauntlet project combines skills in linear algebra, multivariable calculus, and MATLAB programming to have a robot vacuum navigate an obstacle course.

Included in this process is:

• Collecting LIDAR data from the robot vacuum to map out the space the robot vacuum is navigating. This involves applying linear algebra to convert from polar to Cartesian coordinate systems, filter data to remove outliers, and transforming and translating data into different frames of reference.
• Processing of LIDAR data into a map of the space. While individual points are helpful in order to map out the space, continuous lines are needed to navigate based on these paths. To create the boundaries of the walls and objects that need to be navigated around, the LIDAR points are put into a RANSAC algorithm, which provides the benifit of preventing outliers from skewing the line of best fit. This algorithm was coded from scratch in MATLAB
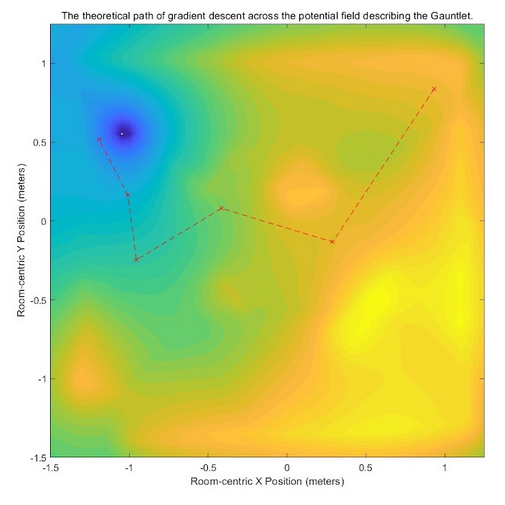
• Creating a path to navigate the course. Based on the boundaries computed using the RANSAC algorithm, the robot actually needs a path from the start point to the end point that avoid these boundaries. First, the computed lines are used to create a vector field, creating local minima at the end point and local maxima around the boundaries. Based upon this vector field, a gradient descent algorithm can be applied, which navigates to the minimum of a function (our end point) by taking steps that decrease in size along the direction of greatest descent in slope until it reaches the minimum of the function (which, in this case, is the end point). This was additionally programed in MATLAB.
• Finally, the robot can be controlled based upon individual wheel velocities to navigate along the path defined by the gradient assent algorithm.

A video of the robot completing this process can be found here: https://www.youtube.com/shorts/fAVC_XoZ3_w